List Of Math Symbols & Their Meaning [Free Downloadable Chart For Classroom]

The list of math symbols can be long. You can’t possibly learn all their meanings in one go, can you? You can make use of our tables to get a hold on all the important ones you’ll ever need. This is an introduction to the name of symbols, their use, and meaning.

Boost your Math skills with FREE Math Apps (Check it NOW)

The Mathematical symbol is used to denote a function or to signify the relationship between numbers and variables. There are many symbols that you might not know the meaning of.

This will help you in improving your algebra skills.

Numbers and symbols form the very basis of mathematics. Math symbols can denote the relationship between two numbers or quantities.

We have ordered the symbols in order of importance for you.

You can also download the ones according to your need.

Table of Content

---

• Basic Math symbols

• Geometry

• Sets Theory

• Calculus and Integration

1. Basic Math Symbols

These are all the mathematical symbols needed to do basic as well as complex algebraic calculations.

list of Math symbols and their meaning:

Symbol	Name	Meaning	Example
=	Equal to	Equality	1+2=3 X=5
≠	Not Equal to	Inequality	X≠5 3+1≠6
≈	Approximately equal to	To approximate	x ≈ y
>	Strict inequality	Greater than	7>1
<	Strict inequality	Lesser than	3<8
≥	Inequality	greater than or equal to	3 ≥ 1 x ≥ 6
≤	inequality	less than or equal to	5 ≤ 5 y≤8
( )	parentheses	calculate expression inside first	3 × (9-2) = 21
[ ]	brackets	calculate expression inside first	[(2+3)×(2+6)] = 40
+	plus	addition	4+1=5
−	minus	subtraction	4-1=3
±	plus – minus	both plus and minus operations	4 ± 6 = 10 or -2
±	minus – plus	both minus and plus operations	5 ∓ 7 = -2 or 10
*	asterisk	multiplication	3 * 4 = 12
×	times sign	multiplication	5×1=5
÷	division sign / obelus	division	15 ÷ 5 = 3
.	multiplication dot	multiplication	2 ∙ 3 = 6
–	horizontal line	division / fraction	8/2 = 4
/	division slash	division	6 ⁄ 2 = 3
mod	modulo	remainder calculation	7 mod 3 = 1
ab	power	exponent	24 = 16
.	period	decimal point, decimal separator	4.36 = 4 +36/100
√a	square root	√a · √a = a	√9 = ±3
a^b	caret	exponent	2 ^ 3 = 8
4√a	fourth root	4√a ·4√a · 4√a · 4√a = a	4√16= ± 2
%	percent	1% = 1/100	10% × 30 = 3
n√a	n-th root (radical)	n√a · n√a · · · n times = a	for n=3, n√8 = 2
%	percent	1% = 1/100	10% × 30 = 3
‰	Per mile	1‰ = 1/1000 = 0.1%	10‰ × 30 = 0.3
ppt	per-trillion	1ppt = 10-12	10ppt × 30 = 3×10-10
ppb	per-billion	1 ppb = 1/1000000000	10 ppb × 30 = 3×10-7

• Download Basic Mathematical Symbols Image Here

2. Geometry

Geometry is the study of shapes and angles. These symbols are used to express shapes in formula mode. You can study the terms all down below.

You might be familiar with shapes and the units of measurements. When starting out with Geometry you should learn how to measure angles and the length of various shapes.

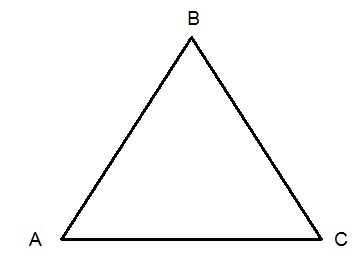
You can use this image to put the below math symbols into context

Symbol	Name	Meaning	Example
∠	Angle	Used to denote a corner of shape	∠ACB of a triangle
∡	Measured Angle	Used to express the value of an angle	∡ACB is 45°
∟	Right Angle	Symbol used instead of ∠ when the angle is 90°	∟ABC is 90°
°	Degree symbol	Measure of angle	20°, 180°
′	prime	arcminute, 1° = 60′	α = 60°59′
″	double prime	arcsecond, 1′ = 60″	α = 60°59′59″
	Infinite line	The line extends at both sides infinitely
	Line segment	A line from point a to point b
	ray	A line that starts from a point and keeps on going
	Arc	Arc from point A to B
⊥	perpendicular	Lines that are 90 degree from a line	⊥
∥	parallel	Lines that are parallel to each other	∥
≅	congruent to	Denotes that the shape and size of one is equal to another	∆ABC≅ ∆XYZ
~	Similar to	Similarity by shape but not size	∆ABC~ ∆XYZ
Δ	Triangle	triangle shape	ΔABC~ ΔBCD
|x–y|	distance	Distance between two points	| x–y | = 3
π	pi	Ratio between circumference and diameter	C=2 . π . r
‘Rad’ or ‘c’	radians	radians angle unit	360° = 2π rad or 360° = 2π c
‘Grad’ or ‘g’	gradians / gons	grads angle unit	360° = 400 grad Or 360° = 400 g

• “Download Geometry Mathematical Symbol For Free”

3. Set Theory

A set is a collection of objects or elements. We can use a set function to find out the relationships between sets. These functions are stated in the table below.

Here is the proper set of math symbols and notations. You should pay attention because these symbols are easy to mix up. Especially ones like intersection and union symbols.

Symbol	Name	Meaning	Example
{}	set	The symbol that encapsulates the numbers of a set	A = {3,7,9,14}, B = {9,12,38}
∩	intersection	objects that are common to two sets	A ∩ B = {9,14}
∪	union	Objects of two sets	A ∪ B = {3,7,9,14,28}
⊆	subset	The contents of one set is derived from another	{9,14,28} ⊆ {9,14,28}
⊂	proper subset / strict subset	A is a subset of B, but A is not equal to B.	{9,14} ⊂ {9,14,28}
⊄	not subset	set A is not a subset of set B	{9,66} ⊄ {9,14,28}
⊇	superset	A is a superset of B. set A includes set B	{9,14,28} ⊇ {9,14,28}
⊃	proper superset / strict superset	A is a superset of B, but B is not equal to A.	{9,14,28} ⊃ {9,14}
⊅	not superset	set A is not a superset of set B	{9,14,28} ⊅ {9,66}
‘2A’ Or ‘P(A)’	power set	all subsets of A
=	equality	both sets have the same members	A={3,9,14}, B={3,9,14}, A=B
Ac	complement	all the objects that do not belong to set A
‘A \ B’ or ‘A – B’	relative complement	objects that belong to A and not to B	A = {3,9,14}, B = {1,2,3}, A-B = {9,14}
‘A ∆ B’ or ‘A ⊖ B’	symmetric difference	objects that belong to A or B but not to their intersection	A = {3,9,14}, B = {1,2,3}, A ∆ B = {1,2,9,14}
a∈A	Elements belongs to	Element of ‘a’ belong to ‘A’	A={3,9,14}, 3 ∈ A
x∉A	not element of	no set membership	A={3,9,14}, 1 ∉ A
(a,b)	ordered pair	collection of 2 elements
A×B	cartesian product	set of all ordered pairs from A and B
‘|A|’ or ‘#A’	cardinality	the number of elements of set A	A={3,9,14}, |A|=3
|	bar	Such that	A={x|3<x<14}
Ø	Empty set	A without any elements	C= Ø
U	Universal set	Set that has all possible elements
N0 and N1	Set of Natural numbers	Set of natural numbers starting from 0 or 1	0 = {0,1,2,3,4,…}   1 = {1,2,3,4,5,…}
Z	Integer set	Set of integer values	= {…-3,-2,-1,0,1,2,3,…}
Q	rational numbers set	= {x | x=a/b, a,b∈}	2/6 ∈ Q
R	real numbers set	= {x | -∞ < x <∞}	6.343434∈ R
C	complex numbers set	= {z | z=a+bi, -∞<a<∞,      -∞<b<∞}	6+2i ∈ C

“Download Set Symbols absolutely free”

4. Calculus and Integration

Calculus helps us understand how the values in a function change. It is a very important concept in math.

For example, calculus can be used to predict the rate of which Covid 19 is spreading. The various values like the number of infected, the number of vulnerable people can be applied to calculus.

Calculus can be a nightmare for you if not studied properly. The calculus and precalculus symbols should be studied in order. From integration to derivation.

Symbol	Symbol Name	Meaning / definition	Example
	limit	limit value of a function
ε	epsilon	represents a very small number, near zero	ε → 0
e	e constant / Euler’s number	e = 2.718281828…	e = lim (1+1/x)x , x→∞
y ‘	derivative	derivative – Lagrange’s notation	(3x3)’ = 9x2
y ”	second derivative	derivative of derivative	(3x3)” = 18x
y(n)	nth derivative	n times derivation	(3x3)(3) = 18
	derivative	derivative – Leibniz’s notation	d(3x3)/dx = 9x2
	second derivative	derivative of derivative	d2(3x3)/dx2 = 18x
	nth derivative	n times derivation
	time derivative	derivative by time – Newton’s notation
	time second derivative	derivative of derivative
Dx y	derivative	derivative – Euler’s notation
Dx2y	second derivative	derivative of derivative
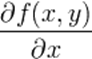	partial derivative		∂(x2+y2)/∂x = 2x
∫	integral	opposite to derivation	∫ f(x)dx
∫∫	double integral	integration of function of 2 variables	∫∫ f(x,y)dxdy
∫∫∫	triple integral	integration of function of 3 variables	∫∫∫ f(x,y,z)dxdydz
∮	closed contour / line integral
∯	closed surface integral
∰	closed volume integral
[a,b]	closed interval	[a,b] = {x | a ≤ x ≤ b}
(a,b)	open interval	(a,b) = {x | a < x < b}
i	imaginary unit	i ≡ √-1	z = 3 + 2i
z*	complex conjugate	z = a+bi → z*=a–bi	z* = 3 – 2i
z	complex conjugate	z = a+bi → z = a–bi	z = 3 – 2i
Re(z)	real part of a complex number	z = a+bi → Re(z)=a	Re(3 – 2i) = 3
Im(z)	imaginary part of a complex number	z = a+bi → Im(z)=b	Im(3 – 2i) = -2
| z |	absolute value/magnitude of a complex number	|z| = |a+bi| = √(a2+b2)	|3 – 2i| = √13
arg(z)	argument of a complex number	The angle of the radius in the complex plane	arg(3 + 2i) = 33.7°
∇	nabla / del	gradient / divergence operator	∇f (x,y,z)
	vector
	unit vector
x * y	convolution	y(t) = x(t) * h(t)
	Laplace transform	F(s) = {f (t)}
	Fourier transform	X(ω) = {f (t)}
δ	delta function
∞	lemniscate	infinity symbol

Be sure to print our table to learn the various math symbols and functions easily.

Download Link

Conclusion

Mathematical symbols allow us to save a lot of time because they are abbreviations. Learning new symbols will allow you to learn more theories and concepts simultaneously.

Boost your Math skills with FREE Math Apps (Check it NOW)

Stick these tables in the classroom or send via Google Classroom so that children can easily get hold of these mathematical symbols.